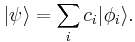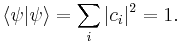Wave function collapse

Quantum mechanics
$\Delta x\, \Delta p \ge \frac{\hbar}{2}$ Uncertainty principle
Introduction Glossary · History
Background Bra-ket notation · Classical mechanics Hamiltonian · Interference Old quantum theory
Fundamental concepts Complementarity · Decoherence Duality · Ehrenfest theorem Entanglement · Exclusion Measurement · Probability amplitude Nonlocality · Quantum state Superposition · Tunnelling Uncertainty · Wave function
Experiments Bell's inequality · Davisson–Germer Delayed choice quantum eraser Double-slit · Elitzur–Vaidman Popper · Quantum eraser Schrödinger's cat · Stern–Gerlach Wheeler's delayed choice
Formulations Formulations Heisenberg · Interaction Matrix mechanics · Schrödinger Sum over histories
Equations Dirac · Klein–Gordon Pauli · Rydberg Schrödinger
Interpretations Consciousness-caused Consistent histories Copenhagen · de Broglie–Bohm Ensemble · Hidden variables Many-worlds · Objective collapse Pondicherry · Quantum logic Relational · Stochastic Transactional
Advanced topics Quantum chaos · Quantum field theory Quantum information science Scattering theory
Scientists Bell · Bohm · Bohr · Born · Bose de Broglie · Dirac · Ehrenfest Everett · Feynman · Heisenberg Jordan · Kramers · von Neumann Pauli · Planck · Schrödinger Sommerfeld · Wien · Wigner

Main article: wave function

In quantum mechanics, wave function collapse (also called collapse of the state vector or reduction of the wave packet) is the phenomenon in which a wave function—initially in a superposition of several different possible eigenstates—appears to reduce to a single one of those states after interaction with an observer. In simplified terms, it is the reduction of the physical possibilities into a single possibility as seen by an observer. It is one of two processes by which quantum systems evolve in time, according to the laws of quantum mechanics as presented by John von Neumann.^[1] The reality of wave function collapse has always been debatable, i.e., whether it is a fundamental physical phenomenon in its own right or just an epiphenomenon of another process, such as quantum decoherence.^[2] In recent decades the quantum decoherence view has gained popularity and is commonly taught at the graduate level (e.g. Cohen-Tannoudji's standard textbook^[3]). Collapse may be understood as an update in a probabilistic model, given the observed result.

1 Mathematical description
- 1.1 Mathematical background
- 1.2 The process of collapse
2 History and context
3 See also
4 Notes

Mathematical description

It is quite simple to describe this phenomenon mathematically - and this leads to the curious philosophical implications and difficulty in understanding what the wave function means.

Mathematical background

For an explanation of the notation used, see Bra-ket notation.

See Quantum state for details on this formalism

The quantum state of a physical system is described by a wave function (in turn – an element of a projective Hilbert space). This can be expressed in Dirac or bra-ket notation as a vector:

$| \psi \rangle = \sum_i c_i | \phi_i \rangle .$

The kets 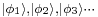$\scriptstyle { | \phi_1 \rangle, | \phi_2 \rangle, | \phi_3 \rangle \cdots }$ , specify the different quantum "alternatives" available - a particular quantum state. Technically they form an orthonormal eigenvector basis, satisfying

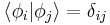$\langle \phi_i | \phi_j \rangle = \delta_{ij}$ .

An observable – i.e. measurable parameter of the system is associated with each eigenbasis, with each quantum alternative having a specific value or eigenvalue, e_i, of the observable. A "measurable parameter of the system" could be the usual position r, time t and momentum p of (say) a particle, but also its energy E, z-components of spin (s_z), orbital (L_z) and total angular (J_z) momenta etc. In the basis representation these are respectively 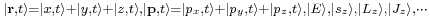$\scriptstyle { | \mathbf{r},t \rangle = | x,t \rangle %2B | y,t \rangle %2B | z,t \rangle, | \mathbf{p},t \rangle = | p_x,t \rangle %2B | p_y,t \rangle %2B | p_z,t \rangle, | E \rangle, | s_z \rangle, | L_z \rangle, | J_z \rangle, \cdots }$ .

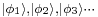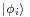The coefficients c₁, c₂, c₃... are the probability amplitudes corresponding to each basis $\scriptstyle { | \phi_1 \rangle, | \phi_2 \rangle, | \phi_3 \rangle \cdots }$ . These are complex numbers. The moduli square of c_i, that is |c_i|² = c_i*c_i (* denotes complex conjugate), is the probability of measuring the system to be in the state $\scriptstyle | \phi_i \rangle$ .

For simplicity in the following, all wave functions are assumed to be normalized; the total probability of measuring all possible states is unity:

$\langle \psi|\psi \rangle = \sum_i |c_i|^2 = 1.$

The process of collapse

With these definitions it is easy to describe the process of collapse. Initially - there are a range of possible outcomes for measurement of the system, any one of the basis states of 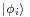$\scriptstyle | \phi_i \rangle$ could appear in the measurement, the relative chances are given by the corresponding probabilities. When an external agency (an observer, experimenter) measures the observable associated with the eigenbasis 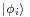$\scriptstyle | \phi_i \rangle$ , the state of the wave function changes from the full 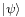$\scriptstyle | \psi \rangle$ to only one of the basis states 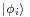$\scriptstyle | \phi_i \rangle$ with Born probability |c_i|², that is:

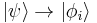$| \psi \rangle \rightarrow | \phi_i \rangle$ .

All the other terms in the expansion of the wave function have vanished into nothing, hence the name "collapse". When the measurement is made - it yields an outcome, only one will occur, even though more than one could, so when it happens no measurement of the other states can subsequently be made.

If a more general measurement is made that detects the system in a state 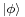$\scriptstyle | \phi \rang$ then the system makes a "jump" or quantum leap from the original state 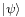$\scriptstyle | \psi \rang$ to the final state 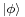$\scriptstyle | \phi \rang$ with probability of 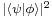$\scriptstyle |\lang \psi | \phi \rang|^2$ . Quantum leaps and wave function collapse are therefore merely two sides of the same coin.

History and context

By the time John von Neumann wrote his treatise Mathematische Grundlagen der Quantenmechanik in 1932,^[4] the phenomenon of "wave function collapse" was accommodated into the mathematical formulation of quantum mechanics by postulating that there were two processes of wave function change:

The probabilistic, non-unitary, non-local, discontinuous change brought about by observation and measurement, as outlined above.
The deterministic, unitary, continuous time evolution of an isolated system that obeys Schrödinger's equation (or nowadays some relativistic, local equivalent, i.e. Dirac's equation).

In general, quantum systems exist in superpositions of those basis states that most closely correspond to classical descriptions, and, when not being measured or observed, evolve according to the time dependent Schrödinger equation, relativistic quantum field theory or some form of quantum gravity or string theory, which is process (2) mentioned above. However, when the wave function collapses (process (1)), from an observer's perspective the state seems to "leap" or "jump" to just one of the basis states and uniquely acquire the value of the property being measured, 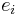$e_i$ , associated with that particular basis state. After the collapse, the system begins to evolve again according to the Schrödinger equation or some equivalent wave equation.

By explicitly dealing with the interaction of object and measuring instrument, von Neumann^[1] has attempted to create consistency of the two processes of wave function change.

He was able to prove the possibility of a quantum mechanical measurement scheme consistent with wave function collapse. However, he did not prove the necessity of such a collapse. Although von Neumann's projection postulate is often presented as a normative description of quantum measurement, it was conceived by taking into account experimental evidence available during the 1930s (in particular the Compton-Simon experiment has been paradigmatic), and many important present-day measurement procedures do not satisfy it (so-called measurements of the second kind).^[5]^[6]^[7]

The existence of the wave function collapse is required in

the Copenhagen interpretation
the objective collapse interpretations
the transactional interpretation
the von Neumann interpretation in which consciousness causes collapse.

On the other hand, the collapse is considered as a redundant or optional approximation in

the Bohm interpretation
the Ensemble Interpretation
the Many-Worlds Interpretation
interpretations based on Consistent Histories

The cluster of phenomena described by the expression wave function collapse is a fundamental problem in the interpretation of quantum mechanics, and is known as the measurement problem. The problem is not really confronted by the Copenhagen Interpretation, which postulates that this is a special characteristic of the "measurement" process. The Many-Worlds Interpretation deals with it by discarding the collapse-process, thus reformulating the relation between measurement apparatus and system in such a way that the linear laws of quantum mechanics are universally valid; that is, the only process according to which a quantum system evolves is governed by the Schrödinger equation or some relativistic equivalent. Often tied in with the Many-Worlds Interpretation, but not limited to it, is the physical process of decoherence, which causes an apparent collapse. Decoherence is also important for the interpretation based on Consistent Histories.

A general description of the evolution of quantum mechanical systems is possible by using density operators and quantum operations. In this formalism (which is closely related to the C*-algebraic formalism) the collapse of the wave function corresponds to a non-unitary quantum operation.

The significance ascribed to the wave function varies from interpretation to interpretation, and varies even within an interpretation (such as the Copenhagen Interpretation). If the wave function merely encodes an observer's knowledge of the universe then the wave function collapse corresponds to the receipt of new information. This is somewhat analogous to the situation in classical physics, except that the classical "wave function" does not necessarily obey a wave equation. If the wave function is physically real, in some sense and to some extent, then the collapse of the wave function is also seen as a real process, to the same extent.

Notes

^ ^a ^b J. von Neumann (1932). Mathematische Grundlagen der Quantenmechanik. Berlin: Springer. (German)

J. von Neumann (1955). Mathematical Foundations of Quantum Mechanics. Princeton University Press. (English)
^ L. Bombelli. "Wave-Function Collapse in Quantum Mechanics". Topics in Theoretical Physics. http://www.phy.olemiss.edu/~luca/Topics/qm/collapse.html. Retrieved 2010-10-13.
^ C. Cohen-Tannoudji (1973; revised 2006). Quantum Mechanics (2 volumes). New York: Wiley. (English)
^ The "collapse" or "reduction" of the wave function was introduced by Heisenberg in his uncertainty paper and later postulated by von Neumann as a dynamical process independent of the Schrodinger equation. C. Kiefer (2002). "On the interpretation of quantum theory – from Copenhagen to the present day". arXiv:quant-ph/0210152 [quant-ph].
^ W. Pauli (1958). "Die allgemeinen Prinzipien der Wellenmechanik". In S. Flügge. Handbuch der Physik. V. Berlin: Springer-Verlag. p. 73. (German)
^ L. Landau and R. Peierls (1931). "Erweiterung des Unbestimmtheitsprinzips für die relativistische Quantentheorie". Zeitschrift fur Physik 69 (1-2): 56. Bibcode 1931ZPhy...69...56L. doi:10.1007/BF01391513. (German))
^ Discussions of measurements of the second kind can be found in most treatments on the foundations of quantum mechanics, for instance, J. M. Jauch (1968). Foundations of Quantum Mechanics. Addison-Wesley. p. 165. ; B. d'Espagnat (1976). Conceptual Foundations of Quantum Mechanics. W. A. Benjamin. pp. 18, 159. ; and W. M. de Muynck (2002). Foundations of Quantum Mechanics: An Empiricist Approach. Kluwer Academic Publishers. section 3.2.4. .